

早 在 公 元 前 600 年 , 在 現 代 文 明 之 源 希 臘 , 生 於 米 利 都 的 希 臘 哲 學 家 塔 利 斯 已 經 提 出 宇 宙 自 有 其 規 律 並 可 為 人 所 了 解 。 大 約 公 元 前 400 年 , 帕 拉 圖 相 信 宇 宙 是 完 美 的 , 而 正 圓 是 最 完 美 的 圖 形 , 所 以 所 有 天 體 皆 應 以 正 圓 運 行 , 而 地 球 則 處 於 宇 宙 的 中 心 , 這 是 地 心 說 的 濫 觴 。
由 於 早 期 的 地 心 說 解 釋 不 了 行 星 逆 行 的 現 象 , 所 以 在 公 元 140 年 , 托 密 勒 提 出 他 的 改 良 版 地 心 說 ( 他 提 出 了 不 少 修 訂 , 但 我 們 只 會 簡 述 他 的 學 說 ) 。

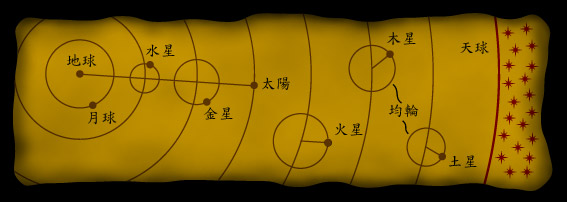
根 據 托 密 勒 的 宇 宙 觀 , 行 星 皆 以 一 個 稱 為 均 輪 的 軌 跡 運 動 , 而 均 輪 的 中 心 則 依 著 一 個 稱 為 本 輪 的 大 正 圓 繞 著 地 球 旋 轉 。 水 星 和 金 星 的 均 輪 中 心 , 和 地 球 及 太 陽 中 心 永 遠 連 成 一 條 直 線 。 眾 星 則 依 附 在 一 個 最 外 層 的 大 天 球 上 。
這 個 理 論 所 預 測 的 行 星 位 置 , 和 實 際 位 置 的 誤 差 在 數 度 之 內 。 當 時 的 人 對 此 已 心 滿 意 足 , 結 果 托 密 勒 地 心 說 主 宰 了 西 方 世 界 約 一 千 五 百 年 。
 | |
| 鳴 謝﹕ 美 國 太 空 總 署 (NASA). |
 | |
| 鳴 謝﹕ 美 國 太 空 總 署 (NASA). |
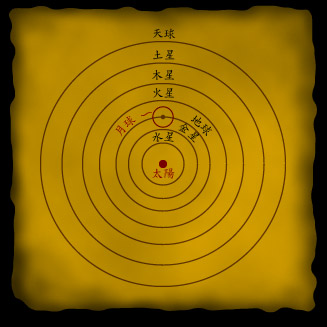
簡 單 來 說 , 伽 利 略 和 梵 蒂 岡 的 衝 突 源 於 伽 利 略 以 觀 測 和 實 驗 來 尋 找 真 理 , 但 僵 化 的 教 廷 卻 認 為 真 理 可 以 在 信 心 中 獲 得 。 宗 教 裁 判 所 最 後 作 出 判 決 , 把 伽 利 略 終 生 監 禁 , 伽 利 略 被 幽 禁 在 一 間 村 屋 之 中 , 度 過 了 他 人 生 中 最 後 的 十 年 。
伽 利 略 是 日 心 說 的 忠 實 擁 護 者 , 也 是 世 上 第 一 個
利 用 望 遠 鏡 窺 探 天 空 的 人 , 這 是 人 類 首 次 在 天
文 上 利 用 儀 器 增 強 自 己 的 觀 測 能 力 。
伽 利 略 有 四 個 主 要 發 現 :
 | |
| 鳴 謝﹕ JPL / 美 國 太 空 總 署 (NASA). |
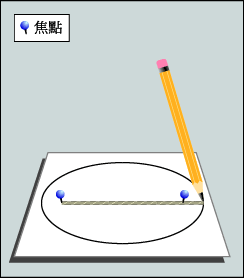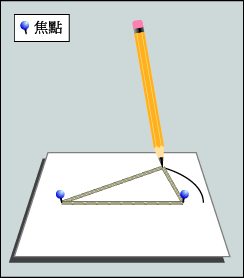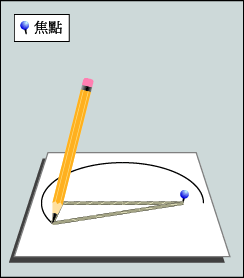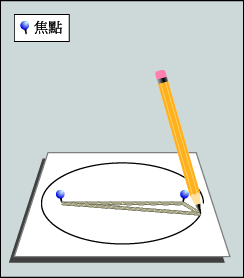
開 普 勒 第 一 定 律 : 所 有 行 星 皆 以 橢 圓 形 軌 道 環 繞 太 陽 運 行 , 而 太 陽 則 處 於 橢 圓 其 中 一 個 焦 點 之 上 。 繪 畫 橢 圓 形 其 中 一 個 方 法 是 固 定 一 條 繩 子 的 兩 端 , 然 後 用 筆 把 繩 繃 緊 , 在 繩 子 拘 束 之 下 , 筆 所 繪 出 來 的 圖 形 便 是 一 個 橢 圓 , 而 繩 子 兩 個 固 定 點 則 是 橢 圓 的 兩 個 焦 點。
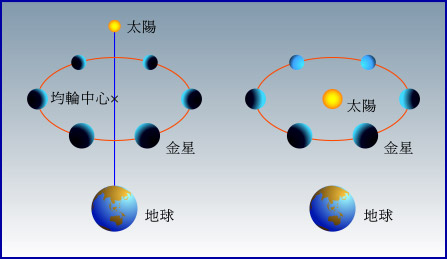
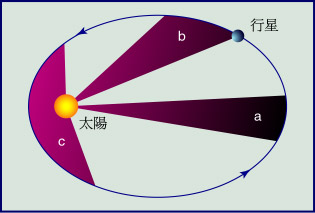
開 普 勒 第 二 定 律 : 假 若 在 行 星 和 太 陽 之 間 畫 一 條 直 線 , 無 論 行 星 在 甚 麼 位 置 , 在 同 等 時 間 之 下 , 這 條 直 線 所 掃 過 的 面 積 皆 會 相 等 。 簡 言 之 , 行 星 越 接 近 太 陽 , 運 行 速 度 越 高 。
開 普 勒 第 三 定 律 : 行 星 公 轉 周 期 的 平 方 和 其 與 太 陽 平 均 距 離 的 立 方 成 正 比 。
公 式 中 常 數 的 數 值 , 對 所 有 行 星 以 至 一 切 環 繞 太 陽 運 動 的 人 造 或 天 然 物 體 皆 適 用 。 假 若 以 地 球 取 代 太 陽 , 例 如 研 究 月 球 或 地 球 人 造 衛 星 時 , 我 們 會 發 覺 上 式 的 常 數 會 有 所 變 更 。
 | |
| 鳴 謝﹕ 美 國 太 空 總 署 (NASA). |
牛 頓 可 以 說 是 現 代 物 理 的 建 基 者 。 雖 然 蘋 果 掉 在 牛 頓 頭 上 , 令 他 悟 出 萬 有 引 力 定 律 的 軼 事 , 很 有 可 能 是 杜 撰 的 , 但 無 論 如 何 , 萬 有 引 力 定 律 無 疑 是 牛 頓 芸 芸 成 就 中 其 中 一 個 重 要 發 現 。
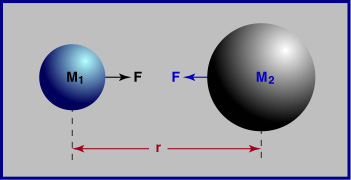
牛 頓 認 為 萬 物 皆 會 互 相 吸 引 , 例 如 原 子 筆 掉 到 地 上 , 便 是 由 於 原 子 筆 和 地 球 互 相 吸 引 。 假 若 兩 件 物 體 的 質 量 分 量 為 M1 及 M2 , 而 它 們 之 間 的 距 離 為 r , 那 麼 它 們 之 間 的 吸 引 力 F 為
公 式 中 的 G 被 稱 為 引 力 常 數 , 是 一 個 非 常 小
的 數 目 , 所 以 當 物 體 的 質 量 很 小 的 時 候 , 它 們 之 間 的
引 力 便 微 不 足 道 , 我 們 看 不 到 日 常 的 物 件 會 互 相 吸 引 ,
例 如 兩 個 人 由 於 萬 有 引 力 而 互 相 碰 撞 ,
便 是 這 個 原 因。
現 在 , 我 們 終 於 明 白 為 甚 麼 月 球 會 環 繞 地 球 運 行 。 如 果 地 球 不 存 在 , 月 球 便 會 以 直 線 運 行 , 飛 向 宇 宙 深 處 。 由 於 地 球 和 月 球 互 相 吸 引 , 月 球 便 向 地 球 靠 攏 , 月 球 不 斷 向 地 球 方 向 落 下 , 而 落 下 的 距 離 剛 好 和 月 球 飛 離 地 球 的 距 離 抵 銷 , 結 果 月 球 便 能 夠 以 接 近 圓 形 的 軌 道 繞 著 地 球 運 行 。 地 球 和 其 他 行 星 也 是 這 樣 不 斷 向 太 陽 落 下 , 才 會 以 現 時 的 軌 道 繞 日 運 行。

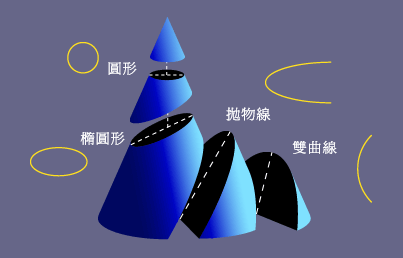
牛 頓 的 引 力 定 律 亦 斷 言 , 星 體 的 軌 跡 除 了 以 直 線 前 進 外 , 也 會 是 四 種 圓 錐 截 線 ─ 圓 形 、 橢 圓 形 、 拋 物 線 或 雙 曲 線 ─ 中 其 中 一 種 。 我 們 稱 這 四 種 形 狀 為 圓 錐 截 線 , 是 由 於 以 不 同 方 法 切 割 圓 錐 體 , 便 可 以 得 到 這 些 形 狀 。 太 陽 系 大 部 分 成 員 以 橢 圓 形 繞 日 運 行 , 但 有 些 彗 星 的 軌 道 則 為 拋 物 線 或 雙 曲 線 。
 |
| 鳴 謝﹕ 美 國 太 空 總 署 (NASA). |
被 譽 為 二 十 世 紀 最 偉 大 的 物 理 學 家 ─ 愛 恩 斯 坦 。 他 從 最 根 本 的 地 方 檢 視 了 牛 頓 理 論 , 然 後 提 出 劃 時 代 的 廣 義 相 對 論 。 現 在 , 我 們 相 信 廣 義 相 對 論 仍 不 是 終 極 真 理 。 科 學 發 展 的 規 律 一 向 如 是 , 有 人 提 出 理 論 , 假 若 它 和 實 驗 結 果 吻 合 , 我 們 便 會 接 受 這 個 理 論 , 但 當 日 後 出 現 更 佳 的 儀 器 , 發 現 理 論 與 新 實 驗 結 果 有 所 偏 差 , 這 個 理 論 便 須 要 再 度 修 正 , 然 後 再 進 行 實 驗 , 循 環 不 息 。