Nature of the Universe

Chapter 5

Telescopes and Electromagnetic Waves

Galileo was the first person who used a telescope to observe the sky. We will see what a telescope is and the nature of light and electromagnetic waves.

Why Do We Need a Telescope?

Most objects in the sky are very dim. Telescope effectively collects more light and converges it for our viewing. Thus, a telescope with larger collecting area, which usually means larger main mirror or lens, is more powerful. This is the main reason why we prefer large telescopes.

Large telescopes also improve the resolution. We can see more clearly even if the apparent size of an object is the same. This is similar, but not equal to, seeing an object in or out of focus.

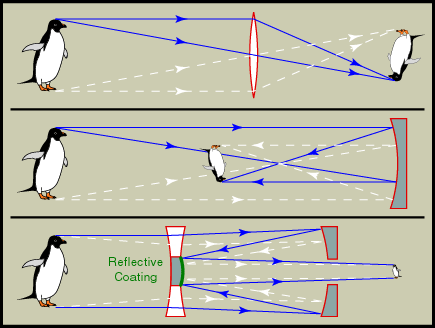
There are three kinds of telescopes: the refracting telescopes (refractors), the reflecting telescopes (reflectors) and the catadioptric telescopes. In refractor, a lens is used to bend light to a point, called the focus, for viewing. In reflector, a mirror is used instead. Catadioptric telescopes use both a lens, called correcting plate, and a mirror. The following figure shows the three basic optical designs of telelscopes.

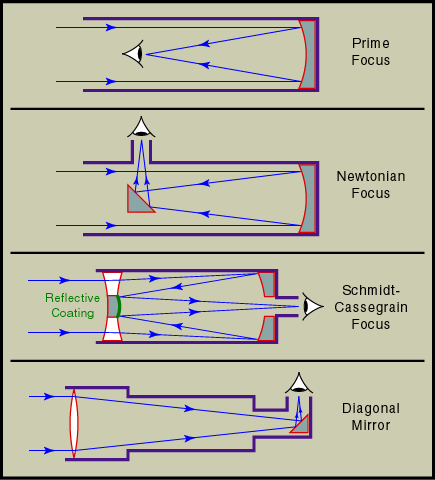
Usually, apart from the main lens or mirror, there are more mirrors to bring the focus to some convenient position, as shown in the diagrams below.

Common misconceptions:

People usually think that larger telescope will magnify the object more. The magnification is the ratio of the apparent sizes of the object. For example, if the angular size of the object is one arc minute and through a telescope, its apparent size becomes 30 arc minutes, then we say the magnification is 30. The magnification of any telescope can be changed very easily (by changing the eyepiece). Even for the largest telescopes, the magnification is seldom over 500, usually between 100 - 200. Thus, large telescopes do not magnify more, they only show brighter and sharper images.
``How far can you see using this telescope?'' This is not a well-defined question. If the object is bright enough, no matter how far it is, we can see it. So, the correct question to ask is ``How dim an object can you see using this telescope?''

The mount of a telescope is also very important. Apart from providing a stable support, a mount should be able to track the stars, that is, to compensate the rotation of the Earth.

So far, we have discussed telescopes for visible light. There are telescopes for radio waves, infrared, X-rays and gamma rays. They can be ground based or orbiting around the Earth. One advantage of the space telescopes is that they will not be affected by the atmosphere, e.g., weather or turbulence. The following is a photo of the largest (in term of collecting area) radio wave telescope, Arecibo, suspended over a valley in Puerto Rico with a diameter of 300 m.

Courtesy NASA.

Properties of Light

We have mentioned radio waves, infrared, visible light, etc. They are all different forms of the electromagnetic wave (EM wave). Like the crests and troughs in water waves, the oscillating electric and magnetic fields constitute an EM wave. The speed of light c is the same for all kinds of EM waves (c=299792450m/s). The distance between successive peaks of one kind of wave is called the wavelength and the number of cycles that pass in one second is the frequency. For EM wave in vacuum, their relation is (wavelength) x (frequency) = c . Each color of the rainbow has some definite frequency.

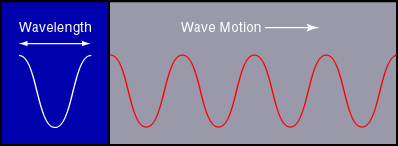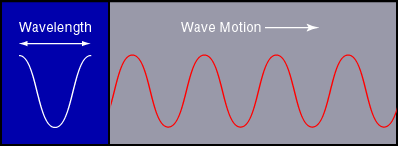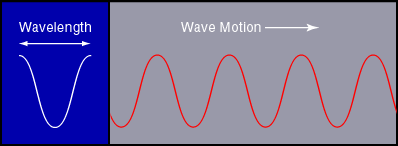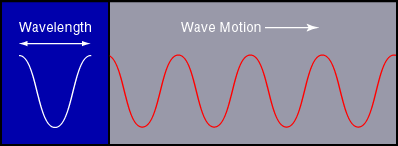
The wavelengths of visible light range from 400 nm to 700 nm. Infrared and radio waves have longer wavelengths but lower frequencies; ultraviolet and gamma ray have shorter wavelengths and higher frequencies. The graph below shows the opacity of our atmosphere to EM waves in different frequencies. We can see that the Earth's atmosphere is opaque to, say, gamma rays and transparent to the visible light. So, we have to put gamma ray telescopes in space.

How can we create light? Just saying ``Let there be light'' will not work very well. However, when we heat something up, it will radiate EM waves. When the object is not very hot, it will be red. If it is hotter, it will be yellow, then white and finally blue.

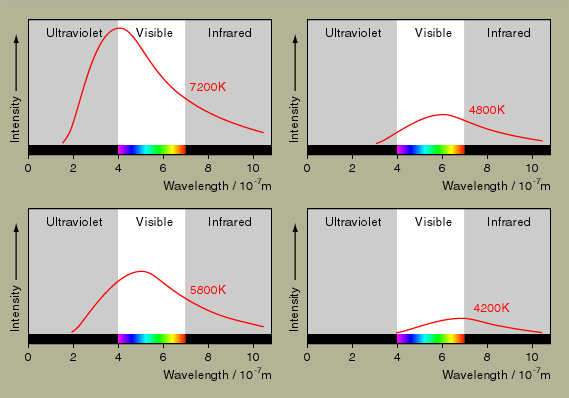
In fact, an object in any temperature will emit EM waves in many frequencies. If we plot the intensity emitted at each frequency, we have the spectrum of the radiation. We call it the black body spectrum. For warm object, the peak of the spectrum is of red color. If it is hotter, it is yellow, etc. Thus, we could tell the surface temperature of a star by its color.

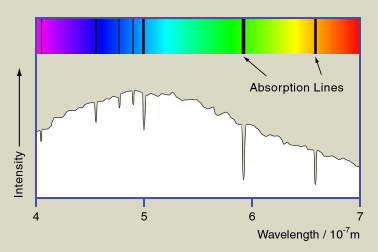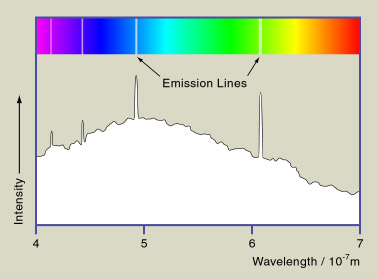
The spectrum in the above figure is continuous in frequency, but it is not always the case. The spectrum from a star could have absorption or emission lines. It is because when atoms are in low pressure, they can only emit or absorb light of certain wavelengths. If some EM wave with continuum spectrum passes through some low pressure atoms (e.g. the outer atmosphere of a star), those atoms will absorb the light it likes and creates an absorption line. Similarly, if some low pressure atoms emit EM wave, they will create emission lines. Different elements will have different sets of lines. By carefully analyzing the spectrum of a star, we can tell which elements the star's surface may contain.

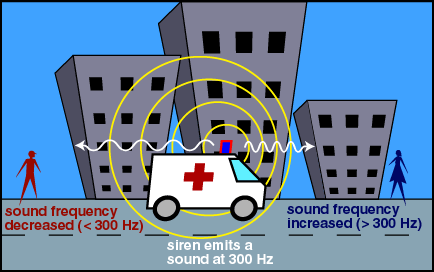
Doppler Effect

When the source of some wave is approaching you, the wave you received will be in a higher frequency (shorter wavelength) compared to the case when the source is stationary. If the source is leaving you, you will see lower-frequency wave (longer wavelength). This is called the Doppler effect. In astronomy, we will call the EM wave blue-shifted or red-shifted, because blue and red are respectively near the frequency of high and low ends of the visible spectrum. If the speed of the source is not large comparing with c, the ratio of the change in wavelength is given by: (observed wavelength - original wavelength) / original wavelength = v / c where v is the velocity of the source leaving you. By comparing the absorption lines from a star to those obtained in a laboratory, we can tell whether the star is moving away or towards us and how fast the star is moving.

Stellar Brightness

We use the visual magnitude, also known as apparent magnitude, to tell others how bright a star is. It is a log scale in intensity. Thus, magnitude and intensity both are scales for brightness of a star. Specifically, if star A is 100 times brighter than star B, then the difference between the magnitudes of A and B is defined to be 5. m_B - m_A = 5 . Note that a dimmer star has a larger magnitude number. We arbitrarily choose one fixed star as the reference and define its magnitude as zero. Then, the magnitude one stars are about 2.51 times dimmer for 2.51⁵=100. Similarly, a magnitude 5 star is 100 times dimmer. The relation between the intensity, I and magnitude, m is m = - 5/2 log ₁₀ ( I / I ₀) . (What is I₀?) The following figure shows the magnitudes of some common objects.

Previous chapter. Next chapter.